Kaggle : Titanic (data profiling _ Seaborn library)
- -
2. seaborn 라이브러리 사용
이전 포스트(matplotlib)에 이어 이번에는 seaborn을 사용하여 막대그래프를 그린다.
seaborn은 카테고리형 (값의 종류가 한정적)일 때 활용하기 좋다.
ⓛ SibSp (동승자 수(형제, 자매, 배우자))와 Survived의 관계
import seaborn as sns
import matplotlib.pyplot as plt
sns.countplot(x='SibSp', hue='Survived', data=train)
plt.legend(loc='upper right', title='survived')- seaborn 라이브러리를 sns라는 이름으로 import한다.
- matplotlib.pyplot 라이브러리를 plt라는 이름으로 import한다.
- sns.countplot()함수
여기서 사용한 파라미터는 3가지이다.
x : x축 변수 (독립변수)
hue : y축 변수 (목적변수)
data : 대상 데이터프레임
- plt.legend() : 범례
(loc : 범례 위치, title : 범례 이름)
결과값:

hist함수와 비슷해보이지만 다르게 표현된다.
두개의 막대가 겹쳐지지 않고, 값의 범위에 따라 count되지 않고 각 값 마다 count된다.
이번 특성은 동승자 수(형제, 자매, 배우자)이다.
특성이름을 보고 떠오르는 가설이 있다.
"혼자 행동하는 것보다는 느릴 가능성이 높기 때문에 동승자 수가 많으면 생존할 가능성이 적다. "
이제 이 가설의 근거를 그래프를 보고 찾아보자.
생존자(1)의 경향(증감 추세)을 보면 0,1,2,3,4로 갈수록 점점 줄어든다.
사망자(0)의 경우 2,3,4에서 거의 동일하거나 4에서 오히려 약간 증가한다.
이를 보면 어느정도 위의 가설의 신빙성을 확인 할 수 있으나 강력하지 않다.
(사망자가 2,3,4에서 증가하는 추세였다면 강력했겠지만...^^)
심지어 증감 추세가 아니라 각 값마다의 대소를 비교했을 때는
동승자 0명일 때 : 사망 > 생존
동승자 1명일 때 : 사망 < 생존
동승자 2명일 때 : 사망 > 생존
동승자 3명일 때 : 사망 > 생존
동승자 4명일 때 : 사망 > 생존
동승자가 1명일 때 오히려 생존자가 많아지는 현상이 보인다.
마치 동승자가 많아지면 생존률이 감소한다는 가설에 반대되는 증거처럼 보인다.
하지만 생각해보자...
1명일 때만 생존자가 오히려 증가한다고 해서 "동승자수가 많으면 생존할 가능성이 적다"는 가설이 무의미한가?
만약 동승자가 1명일때 같이 살아서 나가야겠다는 집념이 오히려 강해졌고
2명 이상일 때는 포기하는 심정이 커졌다면?
기존 가설에 반대되는 증거가 아닌 새로운 유의미한 현상으로 볼 수 있다.
최종 가설을 보자면
"동승자 수가 많을 수록 생존할 가능성이 적다. 하지만 동승자 수가 한명일 때는 오히려 증가한다."
| 이 특성을 모델이 학습할 때 기대되는 효과는 이러하다. 다른 특성들... 동승자수 1명 -> (생존률 +5%) -> 다른특성들.... = 예측값 다른 특성들... 동승자수 2명 -> (생존률 -5%) -> 다른 특성들.... = 예측값 다른 특성들... 동승자수 3명 -> (생존률 -10%) -> 다른 특성들.... = 예측값 |
따라서 Sibsp는 필요한 특성으로 판단된다.
② Parch (동승자 수 (부모, 아이))와 Survived의 관계
sns.countplot(x='Parch', hue='Survived', data=train)
plt.legend(loc='upper right', title='Survived')코드는 거의 동일하므로 설명은 생략.
결과값:

이번 특성은 동승자(부모, 아이)의 수이다.
동승자 (형제, 자매, 배우자) 수였던 이전 특성과 굉장한 양상을 보인다.
이 그래프에서도
"동승자 수가 많을 수록 생존할 가능성이 적다. 하지만 동승자 수가 한명일 때는 오히려 증가한다."
라는 이전에 세웠던 가설이 적용되는지 확인해보자.
인원수의 차이는 있지만 전체적인 경향은 동일하다.
즉 이전에 세웠던 동승자와 관련된 가설이 어느정도 설득력 있다고 볼 수 있다.
이제 동승자와 관련된 가설이 의미있다는 것은 확인됐다.
하지만 여기서 한가지 의문점이자 치명적인 결함이 떠오른다.
(똑똑한 누군가는 위에서 이미 느꼈을 수 도 있다. ^^)
위에서 가설을 세울 때 "동승자가 ~"라고 세웠고, 특히 동승자가 1명일 때 생존률이 증가한다고 했다"
하지만 정확히 말하면
동승자 중 (형제, 자매, 배우자)의 수
동승자 중 (부모, 아이)의 수
이다.
어디가 결함일까?
정답은 중복을 고려하지 못했다는 것이다.
예를 들어 아버지, 어머니, 외동 아들로 구성된 가족이 탑승했다고 가정하자.
특성은 두가지이다. Parch(부모, 아이)와 Sibsp(형제, 자매, 배우자)
아버지의 경우
Parch : 1명
Sibsp : 1명
어머니의 경우
Parch : 1명
Sibsp : 1명
아들의 경우
Parch : 2명
Sibsp : 0명
오류는 아버지, 어머니에게서 발생한다.
아버지와 어머니는 동승자가 1명이라고 2번 학습된다.
이러면 기대되는 학습이 예상과 다르게 흘러간다.
| parch Sibsp 아버지: ........동승자수 1명 -> (생존률 +5%) ->....동승자수 1명 -> (생존률 +5%) => + 10% 어머니: ........동승자수 1명 -> (생존률 +5%) ->....동승자수 1명 -> (생존률 +5%) => + 10% 아들 : ........동승자수 2명 -> (생존률 -10%) ->....동승자수 0명 -> (생존률 + a%) => -10 % + a% |
아버지와 어머니는 결국 동승자가 1명이라고 인식되는 것과 같고,
따라서 아버지와 어머니는 생존률이 두배로 증가한다.
이걸 해결하려면 어떻게 해야 할까..?
두 컬럼의 인원수를 더해서 동승자 수라는 새로운 컬럼을 만들어서 다시 경향을 파악해야 한다.
③ FamilySize (동승자 수)와 Survived의 관계
import seaborn as sns
train['FamilySize'] = train['Parch'] + train['SibSp']
sns.countplot(x='FamilySize', hue='Survived',data=train)train 데이터셋에 'FamilySize'라는 새로운 column을 만들고 값은 train 데이터셋의 'Parch'와 'SibSp'의 값을 합친 값이다.
즉 총 동승자를 뜻한다.
결과값:
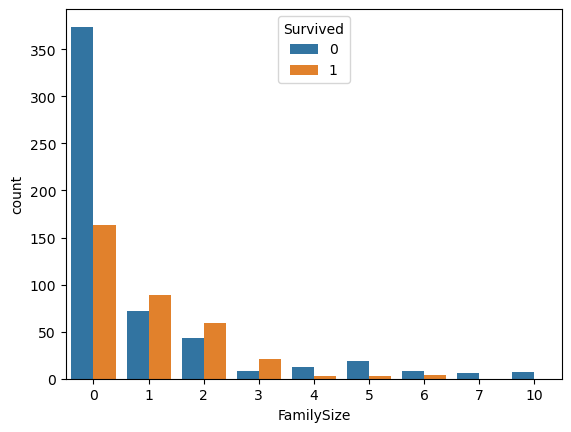
기존 가설을 다시 평가해보자.
"동승자 수가 많을 수록 생존할 가능성이 적다."는 가설은 여기서도 동일하게 적용된다.
하지만
"동승자 수가 한명일 때는 오히려 증가한다."는 가설은 완벽히 기각된다.
따라서 "동승자 수가 많을 수록 생존할 가능성이 적다."는 가설만 성립된다.
| * 추가로 설명할 부분이 있다. 위의 "동승자 수가 많을 수록 생존할 가능성이 적다"라는 가설에 힘을 실어줄 만 한 현상이 있다. 0명일때 0명이 아닌 경우보다 생존자가 많다는 현상이다. 책에서는 동승자가 없을경우(0)인 경우 생존률이 높은 현상을 보고 "동승자가 없으면 생존률이 높다"라는 가설을 세우고 IsAlone이라는 새로운 특성을 만들었다. 하지만 나는 이 행동이 옳지 않다고 생각한다. 일단 코드와 결과를 보자. |
train['IsAlone']=0
train.loc[train['FamilySize']==0, 'IsAlone']=1
sns.countplot(x='IsAlone', hue='Survived', data=train)
| 코드를 간단하게 설명하자면 동승자가 한명이라도 있는 경우 : IsAlone=0 동승자가 없을 경우 : IsAlone=1 경향을 보자. 혼자있을 경우 사망자(파란색)가 더 많다. 하지만 원래 사망자수가 생존자수보다 많아서 그런 것일 수도 있다. 그럼 이번에는 생존자(주황색)을 보자. 생존률(주황색)은 혼자있을 때나, 함께있을 때나 비슷하다. 결론적으로 변별력이 매우 떨어진다는 소리다... 그래프를 수치로 해석하면 더 명확하게 판단할 수 있다. 총 4가지의 조합이 있다 그래프의 순서대로 가족, 사망 : 170 가족, 생존: 170 혼자, 생존 : 170 혼자, 사망 : 350 억지로라도 혼자 생존하는 경우를 강조하고 싶었다면 가중치를 부여해야하지 않았을까...싶다.. 아니다 어차피 원핫인코딩하면 해결될 문제아닌가? 0명일때,1명일때,2명일때... 전부 다른 경우로 학습할 것이고 0명일 경우 생존한 사람이 많았다면 0명이라는 특성을 생존과 가까운 컬럼이라고 인식했을 것이니 말이다. 컴퓨터에서는 이 특성이 '혼자생존하는 경우'라고 인식하지 않는다. 내가 특성이름을 'IsAlone'이 아니라 'A'라고 넣어도 결과는 동일하다. 컴퓨터는 그저 경향을 학습할 뿐이니까.. 특성이름만 들으면 그럴듯해보인다. 가설도 "동승자가 많을수록 생존할 가능성이 적다"이니 맥락도 어느정도 일맥상통한다. 하지만 실상은? 변별력없는 특성같다...ㅎㅎ |
=> FamilySize라는 동승자 수를 의미하는 컬럼 생성, Parch와 SibSp는 제거
④ Sex (성별)과 Survived의 관계
sns.countplot(x='Sex', hue='Survived', data=train)
성별과 생존의 관계는 굉장히 명확하다.
남자가 여자보다 생존률이 매우 높다.
=> Sex 특성 선택
⑤ Embarked (승선한 항구)과 Survived의 관계
sns.countplot(x='Embarked', hue='Survived', data=train)
마지막으로 승선한 항구와 생존과의 관계이다.
동승자 수와는 달리 S,C,Q 간의 대소관계(order or inverval)가 없으므로
각 항구마다의 경향을 개별적으로 살펴 보면
C는 사망한 경우가 많고,
S는 생존한 경우가 많고,
Q는 생존한 경우가 많다.
생존자수와 사망자수의 차이 또한 유의미한 것으로 판단된다.
=> Embarked 특성 선택
저번 포스트의 matplotlib부터 이번포스트의 seaborn까지 파이썬 라이브러리를 활용한 데이터 프로파일링을 알아보았다.
중점!
- 특성간의 관계 파악
- 가설에서의 모순 및 결함 파악
- 가설 수정 및 재검정
- 새로운 특성 생성
+ 새로운 특성을 만들때 주의할 점
다음 포스트부터는 선택한 특성들에 대해 특성 엔지니어링(결측치, 이상치 처리)하는 법에 대해 알아보자.
'데이터 사이언스' 카테고리의 다른 글
| Kaggle : Titanic (Modeling_data set split) (0) | 2023.08.16 |
|---|---|
| Kaggle : Titanic (data preprocessing, feature engineering) (0) | 2023.07.31 |
| Kaggle : Titanic (data profiling _ matplotlib library) (0) | 2023.07.29 |
| Kaggle : Titanic (feature profiling) (0) | 2023.07.29 |
| Kaggle : Titanic (outline) (0) | 2023.07.27 |
소중한 공감 감사합니다